Using mathematics to get the big picture

While imaging techniques have allowed our diagnostic and manufacturing safety standards to flourish, there’s generally trade-offs between accuracy and speed. Often technicians will need to pick either rapid or accurate imaging tools – but what if they could have both rapid and accurate?

Figure 1: Ultrasound image of PI Graff’s baby in 2020 (photo supplied).

As an applied mathematician, Dr Marie Graff translates wave motion and interactions into something usable like images. Mathematically, making a ‘translation’ layer is harder than it sounds, requiring many branches of mathematics to help wrangle quite tricky problems called inverse problems. Once the mathematical translation layer is made, two main tasks remain: (i) have the most accurate model to represent the experiment; (ii) ensure well-posedness (existence, uniqueness and stability of the resulting image) using regularisation techniques.

Where Dr Graff has made a big leap is in using a novel regularisation technique called Adaptive Eigenspace Inversion for a visual example (see Figure 2). Her Marsden project looks at getting a better theoretical understanding of how Adaptive Eigenspace Inversion works. Numerical experiments are showing promising results. Moreover, adding a stochastic dimension, allowed her and the team to quantify how accurate the produced images can be. An additional version of Adaptive Eigenspace Inversion, based on Bayesian inference has also advanced thanks to the work of a Masters student (Tingwei Cheng).

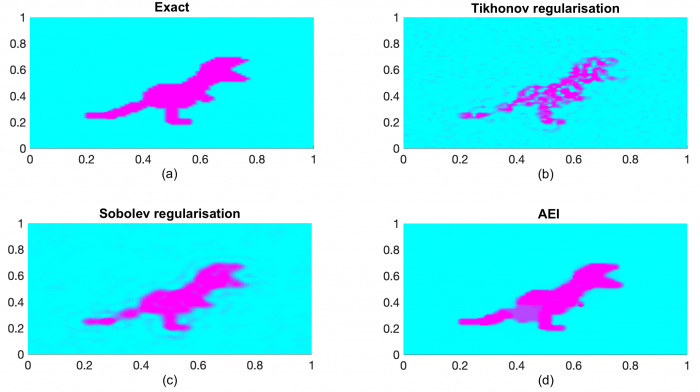
Figure 2: Rawr! A Reconstruction of a dinosaur using three different regularisation techniques: (a) exact image, (b) pointwise reconstruction, (c) smoother reconstruction, (d) AEI reconstruction, highlighting how techniques alter our perceptions of images (photo supplied).

Ultimately Dr Marie Graff and her team are helping us find a ‘sweet spot’ within imaging techniques that don’t always compromise speed and accuracy. Improving our understanding of fundamental mathematics while unlocking numerous benefits across medical and industrial fields – say cheese!